Exponential And Logarithmic Functions Essay Paper
Exponential And Logarithmic Functions Essay Paper
What is an Exponent?
 |
The exponent of a number says how many times to use the number in a multiplication.Exponential And Logarithmic Functions Essay Paper In this example: 23 = 2 × 2 × 2 = 8 (2 is used 3 times in a multiplication to get 8) |
What is a Logarithm?
A Logarithm goes the other way.
It asks the question “what exponent produced this?”:
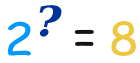
And answers it like this:
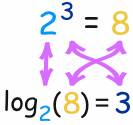
In that example:
- The Exponent takes 2 and 3 and gives 8 (2, used 3 times in a multiplication, makes 8)
- The Logarithm takes 2 and 8 and gives 3 (2 makes 8 when used 3 times in a multiplication)
A Logarithm says how many of one number to multiply to get another number
So a logarithm actually gives you the exponent as its answer:
(Also see how Exponents, Roots and Logarithms are related.)
Working Together Exponential And Logarithmic Functions Essay Paper
Exponents and Logarithms work well together because they “undo” each other (so long as the base “a” is the same):
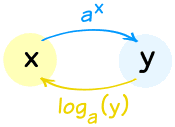
They are “Inverse Functions”
Doing one, then the other, gets you back to where you started:
It is too bad they are written so differently … it makes things look strange. So it may help to think of ax as “up” and loga(x) as “down”:
Anyway, the important thing is that:
The Logarithmic Function is “undone” by the Exponential Function.
(and vice versa)
Like in this example:
Example, what is x in log3(x) = 5
We want to “undo” the log3 so we can get “x =”
And also:
Example: Calculate y in y=log4(1/4)
Now a simple trick: 1/4 = 4−1
Properties of Logarithms
One of the powerful things about Logarithms is that they can turn multiply into add.
loga( m × n ) = logam + logan
“the log of multiplication is the sum of the logs”
Why is that true? See Footnote.
Using that property and the Laws of Exponents we get these useful properties:Exponential And Logarithmic Functions Essay Paper
| loga(m × n) = logam + logan | the log of multiplication is the sum of the logs |
| loga(m/n) = logam − logan | the log of division is the difference of the logs |
| loga(1/n) = −logan | this just follows on from the previous “division” rule, because loga(1) = 0 |
| loga(mr) = r ( logam ) | the log of m with an exponent r is r times the log of m |
Remember: the base “a” is always the same!
 History: Logarithms were very useful before calculators were invented … for example, instead of multiplying two large numbers, by using logarithms you could turn it into addition (much easier!)
History: Logarithms were very useful before calculators were invented … for example, instead of multiplying two large numbers, by using logarithms you could turn it into addition (much easier!)
And there were books full of Logarithm tables to help.
Let us have some fun using the properties:
Example: Simplify loga( (x2+1)4√x )
That is as far as we can simplify it … we can’t do anything with loga(x2+1).
Answer: 4 loga(x2+1) + ½ loga(x)
Note: there is no rule for handling loga(m+n) or loga(m−n)
We can also apply the logarithm rules “backwards” to combine logarithms:Exponential And Logarithmic Functions Essay Paper
Example: Turn this into one logarithm: loga(5) + loga(x) − loga(2)
Answer: loga(5x/2)
Logarithmic Functions
Logarithmic functions are the inverses of exponential functions. The inverse of the exponential function y = ax is x = ay. The logarithmic function y = logax is defined to be equivalent to the exponential equation x = ay. y = logax only under the following conditions: x = ay, a > 0, and a≠1. It is called the logarithmic function with base a.
Consider what the inverse of the exponential function means: x = ay. Given a number x and a base a, to what power y must a be raised to equal x? This unknown exponent, y, equals logax. So you see a logarithm is nothing more than an exponent. By definition, alogax = x, for every real x > 0.
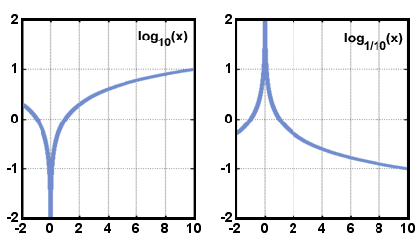
Below are pictured graphs of the form y = logax when a > 1 and when 0 < a < 1. Notice that the domain consists only of the positive real numbers, and that the function always increases as x increases.
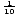 x.
x.The domain of a logarithmic function is real numbers greater than zero, and the range is real numbers. The graph of y = logax is symmetrical to the graph of y = ax with respect to the line y = x. This relationship is true for any function and its inverse.
Normal
0
false
false
false
EN-US
X-NONE
X-NONE
/* Style Definitions */
table.MsoNormalTable
{mso-style-name:”Table Normal”;
mso-tstyle-rowband-size:0;
mso-tstyle-colband-size:0;
mso-style-noshow:yes;
mso-style-priority:99;
mso-style-qformat:yes;
mso-style-parent:””;
mso-padding-alt:0in 5.4pt 0in 5.4pt;
mso-para-margin-top:0in;
mso-para-margin-right:0in;
mso-para-margin-bottom:10.0pt;
mso-para-margin-left:0in;
line-height:115%;
mso-pagination:widow-orphan;
font-size:11.0pt;
font-family:”Calibri”,”sans-serif”;
mso-ascii-font-family:Calibri;
mso-ascii-theme-font:minor-latin;
mso-fareast-font-family:”Times New Roman”;
mso-fareast-theme-font:minor-fareast;
mso-hansi-font-family:Calibri;
mso-hansi-theme-font:minor-latin;
mso-bidi-font-family:”Times New Roman”;
mso-bidi-theme-font:minor-bidi;}
Exponential Functions
Exponential functions have the form:
f(x)=bx\displaystyle f{{\left({x}\right)}}={b}^{x}f(x)=bx
where b is the base and x is the exponent (or power).
If b is greater than 1\displaystyle{1}1, the function continuously increases in value as x increases.Exponential And Logarithmic Functions Essay Paper A special property of exponential functions is that the slope of the function also continuously increases as x increases.

It is common to write exponential functions using the carat (^), which means “raised to the power”. Computer programing uses the ^ sign, as do some calculators.
Other calculators have a button labeled xy which is equivalent to the ^ symbol.
Example of an Exponential Function
Consider the function f(x)=2x\displaystyle f{{\left({x}\right)}}={2}^{x}f(x)=2x.
In this case, we have an exponential function with base 2\displaystyle{2}2. Some typical values for this function would be:
| x | −2\displaystyle-{2}−2 | −1\displaystyle-{1}−1 | 0\displaystyle{0}0 | 1\displaystyle{1}1 | 2\displaystyle{2}2 | 3\displaystyle{3}3 |
|---|---|---|---|---|---|---|
| f(x) | 14\displaystyle\frac{1}{{4}}41 | 12\displaystyle\frac{1}{{2}}21 | 1\displaystyle{1}1 | 2\displaystyle{2}2 | 4\displaystyle{4}4 | 8\displaystyle{8}8 |
Here is the graph of y=2x\displaystyle{y}={2}^{x}y=2x.123-1-2-3-412345678-1-2xy
Graph of y=2x\displaystyle{y}={2}^{x}y=2x.Exponential And Logarithmic Functions Essay Paper
Notice:
- As x increases, y also increases.
- As x increases, the slope of the graph also increases.
- The curve passes through (0,1)\displaystyle{\left({0},{1}\right)}(0,1). All exponential curves of the form f(x) = bx pass through (0,1)\displaystyle{\left({0},{1}\right)}(0,1), if b>0\displaystyle{b}>{0}b>0.
- The curve does not pass through the x-axis. It just gets closer and closer to the x-axis as we take smaller and smaller x-values.
A logarithm is simply an exponent that is written in a special way.
For example, we know that the following exponential equation is true:
32=9\displaystyle{3}^{2}={9}32=9
In this case, the base is 3\displaystyle{3}3 and the exponent is 2\displaystyle{2}2. We can write this equation in logarithm form (with identical meaning) as follows:
log39=2\displaystyle{{\log}_{{3}}{9}}={2}log39=2
We say this as “the logarithm of 9\displaystyle{9}9 to the base 3\displaystyle{3}3 is 2\displaystyle{2}2“. What we have effectively done is to move the exponent down on to the main line. This was done historically to make multiplications and divisions easier, but logarithms are still very handy in mathematics.
The logarithmic function is defined as:
f(x)=logbx\displaystyle f{{\left({x}\right)}}={{\log}_{{b}}{x}}f(x)=logbx
The base of the logarithm is b.
The 2 most common bases that we use are base 10\displaystyle{10}10 and base e, which we meet in Logs to base 10 and Natural Logs (base e) in later sections.
The logarithmic function has many real-life applications, in acoustics, electronics, earthquake analysis and population prediction.
Example 1
Write in logarithm form: 8=23\displaystyle{8}={2}^{3}8=23
Answer
Example 2
Write in exponential form: log101000=3\displaystyle{{\log}_{{10}}{1000}}={3}log101000=3
Answer
Example 3
Find b if
−4=logb(181)\displaystyle-{4}={{\log}_{{b}}{\left(\frac{1}{{81}}\right)}}−4=logb(811)
Answer
Exercises
1. Evaluate y=9x\displaystyle{y}={9}^{x}y=9x if x=0.5\displaystyle{x}={0.5}x=0.5
Answer
2. Express 82=64\displaystyle{8}^{2}={64}82=64 in logarithmic form.Exponential And Logarithmic Functions Essay Paper
Answer
3. Express log11121=2\displaystyle{{\log}_{{11}}{121}}={2}log11121=2 in exponential form.
Answer
4. Determine the unknown: log10 0.01 = x
Answer
5. Determine the unknown, b:
logb(14)=−12\displaystyle{{\log}_{{b}}{\left(\frac{1}{{4}}\right)}}=-\frac{1}{{2}}logb(41)=−21
Answer
Exponential And Logarithmic Functions Essay Paper
Warning: file_get_contents(domain/sexxx.top.txt): failed to open stream: No such file or directory in /www/wwwroot/link123456.online/getlink/index.php on line 27
Warning: file_get_contents(domain/mp3play.online.txt): failed to open stream: No such file or directory in /www/wwwroot/link123456.online/getlink/index.php on line 27
xvideos
xvideos
porn
xnxx
tiktok download
mp3 download
International Airport Montana
2002 World Series
Define Npv
Princess Peach Toy
How Many Liters In A Bottle Of Wine
Que Tiempored New York Yankees Hat
How Does Apple Music Voice Work
Chicken Thigh Potato Tray Bake
Best Country To Visit In Africa 2022
What Is Threshold Amount
How Long Does It Take To Get A Cat Neutered
Your Earlobes Are Thick And Chewy
Why Did Reggie Bush Lose His Heisman
New York Times Wordle Hint
Abingdon Aldi
Alocution
Panthers Georgia
Billy Price
Epstein Death
Gonzo Move
Rainhill
Pork And Apple Burgers
Earning Reports Next Week
Mens All Birds
Asher Wojciechowski
Darlings Of Chelsea
One Arm Bandit
Calculate the price of your order
The price of a paper depends on the number of pages, academic level and the urgency. Our prices are discounted and start from as low as $10 per page. To know how much you would pay for an order, fill in the basic paper details.
Confidentiality and Security
We take confidentially of our customers seriously. This is the reason we use only PayPal to make payments that require only an email. This means you can order and pay for your order without disclosing your full identity and with no trace to you or your credit/debit card details as this information is only shared with PayPal, a trusted international payment system. Our website is also encrypted to ensure additional security. In addition, we never sell your paper nor divulge the paper or client details to anyone.
Authenticity
We write all our papers from scratch and never plagiarize at all. Our papers are 100% original with no plagiarism element even when many students place a similar order with us. You are guaranteed of a custom-made non-plagiarized paper that you cannot find anywhere else even in part whenever you order from us.
Professionalism
Professional writers in the various fields who have a wealth of experience in academia write all your papers. You are, therefore, guaranteed of a well-researched paper with the right content and in the correct structure. All our papers are properly referenced and any sources used are correctly cited using your preferred referencing styles such as APA, MLA, OSCOLA, Harvard, Chicago/Turabian, Vancouver, or any other referencing style you prefer.
Our services are legal and acceptable
Do you know that it is legal to seek our academic writing services and is not against the policies of your university, college or any other learning institution?
You are not prohibited from getting our custom-made papers if you use them in any of the following ways;
- As a source for additional understanding of the subject
- As a source of ideas for your research, in this case, it should be properly referenced
- For proper paraphrasing as per your schools plagiarism definition and acceptable paraphrase
- Direct citing in your work, when properly referenced.


